Pipeline using non-blocking assignment

Implements \(\{(A_0 + A_1) << (A_3-A_4)\} + 22\) as three stage pipeline:

Stages:

  1. Add \(A_0\) to \(A_1\), subtract \(A_4\) from \(A_3\) and assign the values to \(t_0\) and \(t_1\) respectively.
  2. Left shift \(t_0\) by \(t_1\).
  3. Add 22 to the result from stage 2.
/* Implements ((din0 + din1) << (din2 - din3)) + 22 */
module pipeline
  (
   input 	       clk_in,
   input logic [31:0]  din0,
   input logic [31:0]  din1,
   input logic [31:0]  din2,
   input logic [31:0]  din3,
  
   output logic [31:0] dout);

   logic [31:0]        sum_T1;
   logic [31:0]        diff_T1;

   logic [31:0]        res_T2;
   
   always @(posedge clk_in) begin
      /* Stage 1 */
      sum_T1  <= din0 + din1;
      diff_T1 <= din2 - din3;

      /* Stage 2 */
      res_T2  <= sum_T1 << diff_T1;

      /* Stage 3 */
      dout    <= res_T2 + 22;
   end
endmodule

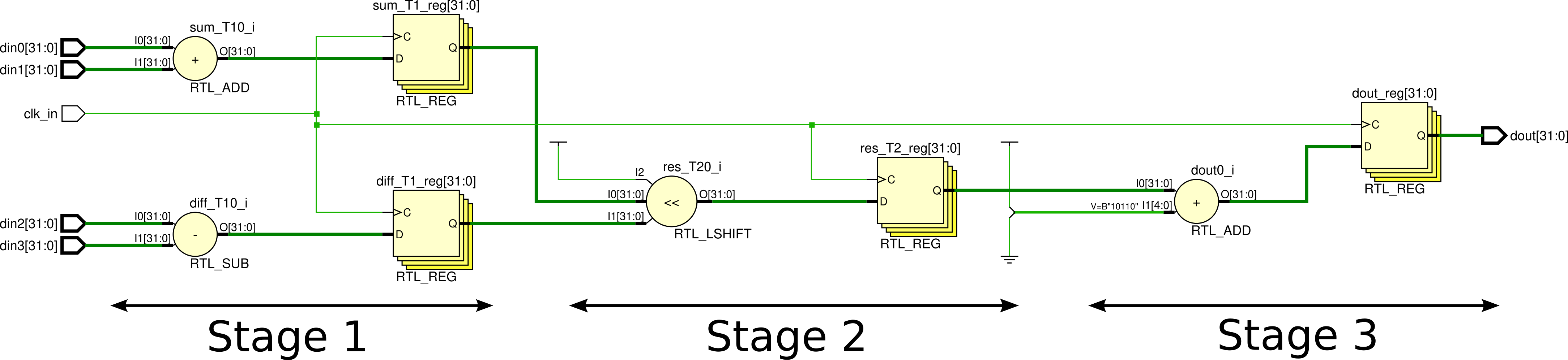
Elaborated design: Pipeline schematic

Synthesis using for-loops

Pipeline implementation using for loops

`timescale 1ns / 1ps

module fifo
  #(
    parameter DATA_W = 32,
    parameter Q_DEPTH = 4
    )(
      input 		  clk_in,
      input [DATA_W-1:0]  din,
      input 		  din_en,
      
      output [DATA_W-1:0] dout
      );

   logic [DATA_W-1:0] 	  queue [Q_DEPTH-1:0];
   integer 		  i;

   assign dout = queue[Q_DEPTH-1];

   always @(posedge clk_in) begin
      if (din_en) begin
	 queue[0] <= din;

	 for (i = 1; i < Q_DEPTH; i = i+1) begin
	    queue[i] <= queue[i-1];
	 end
      end
   end
   
endmodule